Activities about the transit of Venus

Here are some possible activities on the transit of Venus which can be adapted according to the pupils’ level and the purpose which is to reach.
We could for instance carry out a scale model of the transit of Venus by giving the dimensions which are already calculated. The Sun will be represented by a basket ball, the Earth and Venus by a pinhead.

1. A scale model

We want to carry out a model on a scale of 1 to 6 000 000 000 of the transit of Venus on June, 6th 2012.

Calculate the diameters of the Earth, of Venus and the Sun as well as the distances to the Earth, Venus and the Sun on this scale.

The data:

• Radius of the orbit of Venus : 108 000 000 km. Diameter of Venus : 12 100 km.
• Radius of the orbit of the Earth : 150 000 000 km. Diameter of the Earth : 12 800 km.
• Diameter of the Sun : 1 400 000 km.

2. Apparent diameters of Venus and of the Sun.

When Venus is going to pass in front of the Sun, it will appear smaller then the sun. But how many times smaller?

The data:

• Radius of the orbit of Venus: 108 000 000 km. Diameter of Venus : 12 100 km.
• Radius of the orbit of the Earth : 150 000 000 km. Diameter of the Earth : 12 800 km.
• Diameter of the Sun : 1 400 000 km.

3. Maximum duration of a transit.

Calculate the approximate maximum duration of a transit of Venus in front of the Sun.

The data

• Radius of the orbit of Venus: 108 000 000 km.
• Radius of the orbit of the Earth: 150 000 000 km.
• Diameter of the Sun: 1 400 000 km.
• Duration of synodic revolution of Venus: 584 days.

Solutions

1. A scale model

On a scale of 1 to 6 000 000 000

• Radius of the orbit of Venus : 18 m. Diameter of Venus : 2 mm.
• Radius of the orbit of the Earth : 25 m. Diameter of the Earth : 2 mm.
• Diameter of the Sun : 23,3 cm

2. Apparent diameters of Venus and the Sun

We can calculate the apparent diameters of Venus and the Sun, either by calculating the arctangent function arc or by using the radians or by comparing the diameter of the aster to an arc of circle.
Apparent diameter of the Sun: 1 396 000 km seen from 150 000 000 km which gives an angle in degree equalling:
1 396 000 / 150 000 000 × 180 / 0,533°
Apparent diameter of Venus: 12 100 km seen from 42 000 000 km which gives an angle in degree equalling :
12 100 / 42 000 000 × 180 / 0,0165°
So Venus appears 32 times smaller than the Sun (0,533/0,0165).

We can find directly the result by calculating 1 366 000/12 100 × 42 000 000/150 000 000

3. Maximum duration of a transit.

So that the duration of the transit is maximum, we can suppose that Venus passes in front of the center of the Sun .

Seen from the Earth, we can see Venus turn around the Sun with a period of 584 days.

The reference axis, which is considered fixed is the axis Earth-Sun. It is the simplest landmark as the observer is on the Earth which is considered fixed.

All the calculations will be made in this landmark. The observer is set at the centre of the Earth. We consider that Venus follows a circular trajectory at a constant speed. Thus we will get an approximate result.

Speed of Venus on its orbit: 108 000 000 km × 2 ×Π/ 584 days 1 132 000 km/d or 48 400 km/h.

Distance that Venus must cover during a transit (Venus is considered punctual).


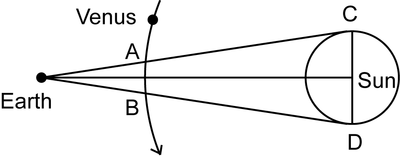
AB/CD = EA/EC
By making a few approximations, we can find: AB 392 000 km.
It takes Venus about 8 hours to cover this distance at the speed of 48 400 km/h.
So the maximum duration of a transit is about 8 h.