Eratosthenes's experiment
Eratosthenes (276-194 BC) succeeded in measuring with a very simple way the circumference of the Earth
The aim of this activity is to use a similar method to measure the circumference of the earth.
First challenge
|
Measure the height and the azimuth of the Sun as accurately as possible. 1. Knowing that we cannot look at the Sun directly, propose a simple experiment for viewing altitude and theazimuth(see definitionsin the dictionary). Make a list of the necessary equipment. 2. The teacher gives the following equipment: a polystyrene board, a stick wood, a compass, a level, a ruler, a piece of paper, a square, the experiment takes place in a yard with gravels. a) Drafting a protocol for the measurement of the position of the Sun. Be verified by the teacher b) Achieve the measure, noting also the time at which you have done it c) What are the phenomena that make inaccurate measurement? |
 |
| What do we need for this experiment. |

The experiment ready to use on the ground.
Second challenge: Measuring the circunference of the Earth
Thanks to the shade of a stick, Eratosthenes was able to measure the circumference of the Earth. We work, with a similar method, on measurements carried out on the day of the Equinox.
1) Students from different countries decide to measure at the same time the position of the Sun in the shade of a stick. The experience is drawn below (the drawing is not to scale). Represent the shadow of the for sticks on the drawing below.
2) Features of the Equinox:
|
The Equinox in took place this year (2010) on September 23. Complete: On the Equinox, on the Earth, the duration of the day is ……….. that the duration of the night. Another particularity of the Equinox: atsolar noon , the Sun is at the Zenith, i.e. to the vertical from the equator. What then is the length of the shadow of a stick placed vertically at the Equator? |
 |
| A model to explain the size of the shadow according to the latitude (during the equinox day) |
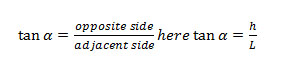 )
) |
 |
| We plot the end of the shadow | Details of the shadows |
| Determine the relationship between the angle determined previously and the angle between the radius of the Earth at the Equator and our school location in Décines (see the diagram on the right.) | 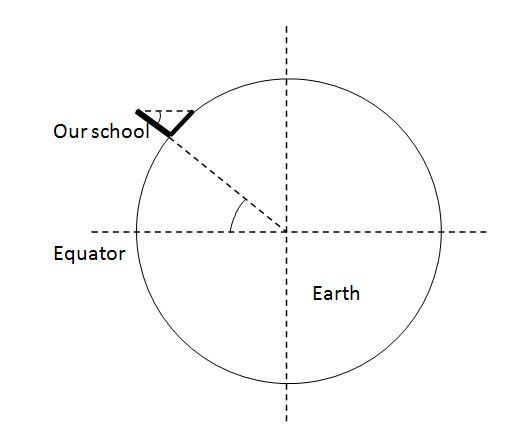 |
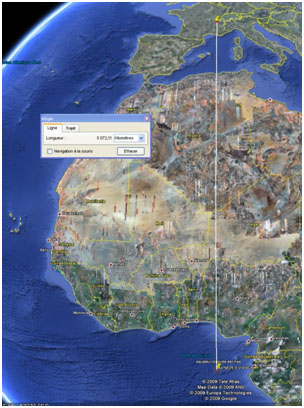
5) In the "Google Earth" software can measure the distance between the Equator and our school location in Décines, we find d=5070km
 |
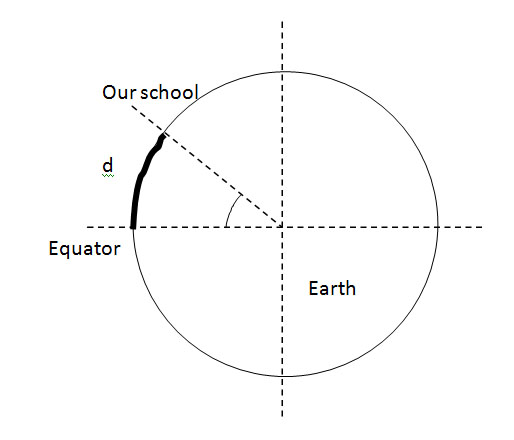 |
6) From the properties of the circle, determine the perimeter p of the Earth.
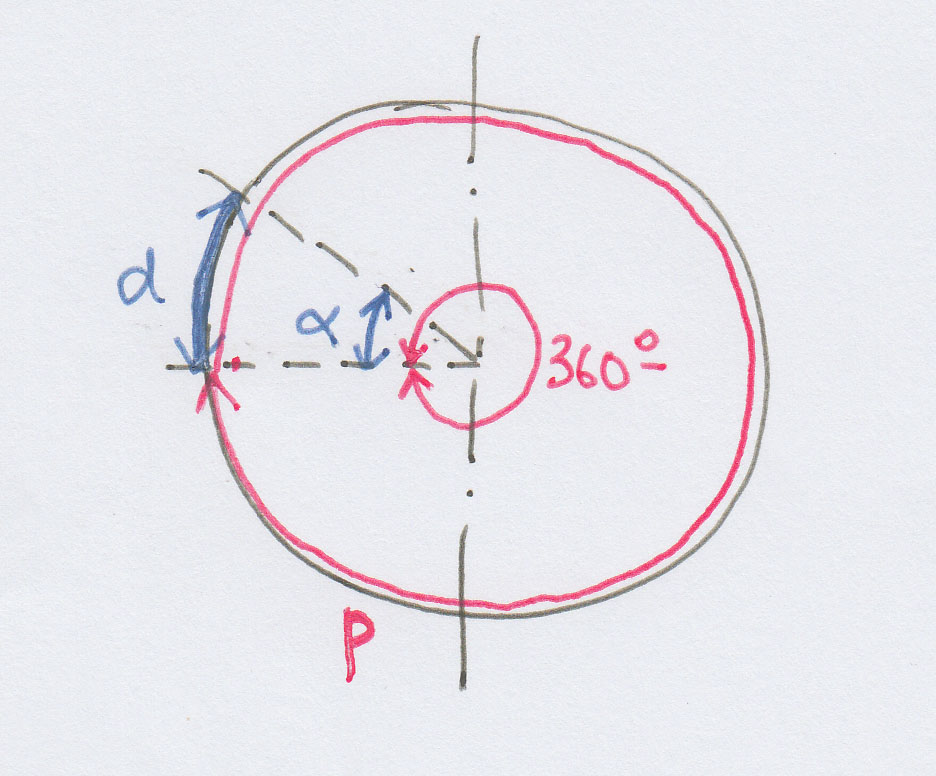
Calculations for participants
Links
La main à la Pâte
European Association for Astronomy in Education : Eratosthenes
Le site Eratosthène du Collège Antonin Perbosc de Lafrançaise
- Galery of gnomons english espanol french
- Seasons with Geogebra
- Geometrical Ephemérides with Geogebra
Document Actions

