Calculating the distance of the Sun with the transit of Venus of June 8, 2004
On June, 8 2004, we could see Venus pass in front of the Sun. This transit hadn’t occurred since 1882. Let’s calculate the distance of the Sun thanks to the photographs taken on the day of that event.
French version : Comité de Liaison Enseignants Astronomes
First part
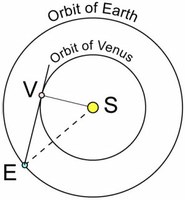
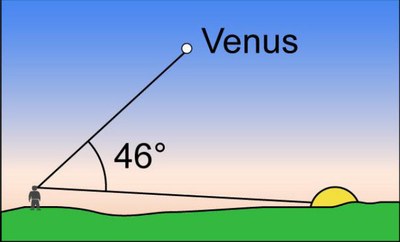
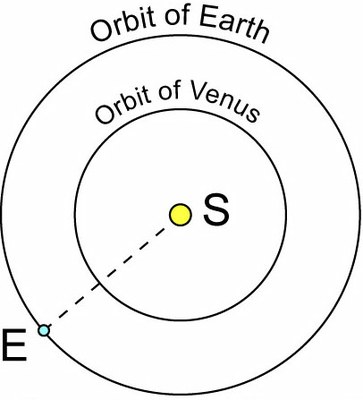
Venus is often visible in the evening or morning and it is very luminous. It was nicknamed the shepherd’s star but it is a planet, which goes around the Sun. Its observation enables us to calculate the relative dimensions of the orbits of Venus and the Earth.
Seen from the Earth, Venus never ventures further than 46° from the Sun, which is called the maximum elongation.
Second part
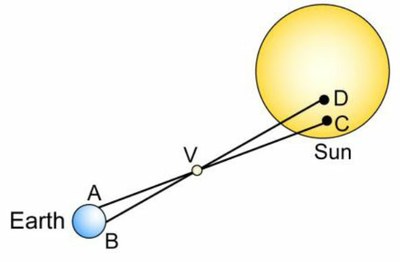 |
By observing a transit of Venus in front of the Sun at two distant places, we can calculate the distance of the Sun. Principle: the observers situated on the Earth in A (in Dijon) and B (Réunion Island) can see Venus in front of two different points of the Sun, C and D. |
a. The two photos were taken exactly at the same time (8.30 am Universal Time) and oriented in the same way (the north at the top).
 |
 |
|
The Sun and Venus photographed in St Louis (Reunion Island) on June 8 2004 at 8.30 am UT) |
Venus photographed in Dijon on June 8 2004 at 8.30 am UT (Universal Time) |
| Superimpose these two photos then determine the gap in degrees between the two pictures of Venus knowing that the apparent diameter of the Sun was 0.525 ° that day. | 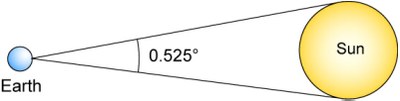 |
b. After measuring the azimuth and the height of the Sun at 8.30 am UT in Dijon, we could materialize on this globe the direction of the Sun observed in La Reunion and Dijon.
| Determine the distance between these two lines of sight knowing that the diameter of the Earth is 12 740 km. (To take the right photo, the photographer took up this position so as to make the line of sight perpendicular to the plane including the two sticks.) |
 |
c. (AB) and (CD) are considered perpendicular to the line( Earth-Sun)
 |
| By using the results to the questions 1b and 2b, calculate CD. |
d. We have just got the measurement of CD in km. We have found in the question 2a under which angle we could see CD. We can now calculate how far from the sun we must take our positions to see the length CD under the angle determined in 2a. We will then have the distance Earth/Sun.
The photos (both photos are on the same scale and oriented in the same way, the north at the top).
Correction and remarks.
First part
Second part
a. The sun’s diameter in the photo is 114 mm for 0.525° so the scale is 0,0046°/mm. In this kind of exercises, we consider that the measurement of a segment is proportional to the angle under which we can see it from the Earth. It is true for the measurement of the arcs of circle centred on the Earth so here it comes down to assimilate the segment to the arc of circle. As the angles are small (inferior to a degree), the mistake is negligible.
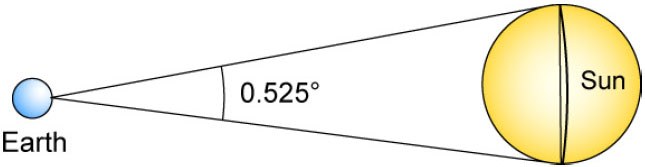
When we superimpose the two photos with a tracing paper, we get a gap of 1.5 to 2 mm between the two images of Venus, which makes 0.0069 to 0.0092° with our scale. We can be more precise by using the digitized pictures (on the CLEA site) and superimposing them with a software programme. We find about 0.0086°.
b. Diameter of the Earth in the photo : 39 mm for 12740 km
Measured gap between the two sticks in the picture : 25 mm, which corresponds to about 8200 km.
c. We have considered (AB) and (CD) perpendicular to the straight line Earth-Sun (the straight line passing though the centres of these two asters) so they are parallel to each other and the famous Thales’ theorem enables us to find CD. The result to this question 1a (SV/ST=0.72) enables us to write: CV= 0.72 CA so VA=0.28 CA and CV/CA=0.72/0.28.
Besides with AB=8200 km, we get CD= 21 100 km………
d. Last stage:
we still have to find how far we are from the Sun to see a segment of 21 100 km under an angle of 0.0086°.
Several methods are possible:
With proportions (by assimilating the segment of 21 100 km to an arc of circle centred on the observer) :

0.0086° ![]() 21 100 km. By dividing by 0.0086 then y multiplying by 360 :
21 100 km. By dividing by 0.0086 then y multiplying by 360 :
360°![]() 880 000 000 km. By dividing by 2
880 000 000 km. By dividing by 2  , we get a distance of about 140 000 000 km.
, we get a distance of about 140 000 000 km.
This calculation can be made as well by using a tangent or also by transforming the angle in radians
e. Precision :
Considering the precision of the orientation of the pictures, the scaling and the measurements, we can admit that the uncertainty of the calculations can’t exceed 20 %.
If we compare with the official distance (it was 151 800 000 km that day), the distance we got is underestimated by 8 %. It is not that bad but we could have been more precise with more careful shots.
Conclusion:
we can say that the distance Earth-Sun is between 110 and 170 million km. It is not very precise but getting a correct order of magnitude of the distance Earth-Sun is not bad at all!
Document Actions

 0.72
0.72