Mathematics
Wordings
1. Venus and Earth in their orbits
Prerequisite knowledge : scales, drawing angles
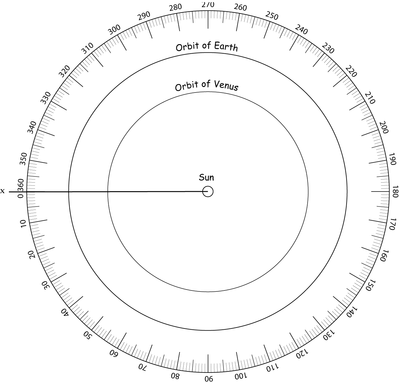
We wish to represent the positions of Venus and Earth in early 2012. The distance from the Sun to Venus is 108 million km from the Sun to the Earth is 150 million km.
Chosen scale is 1 cm to 20 million km.
- Calculate the distances Sun-Venus and Sun-Earth on this scale.
- On a sufficiently large sheet of paper, mark a point S to represent the Sun and then represent the orbits of Venus and the Earth using circles centred on S on this scale.
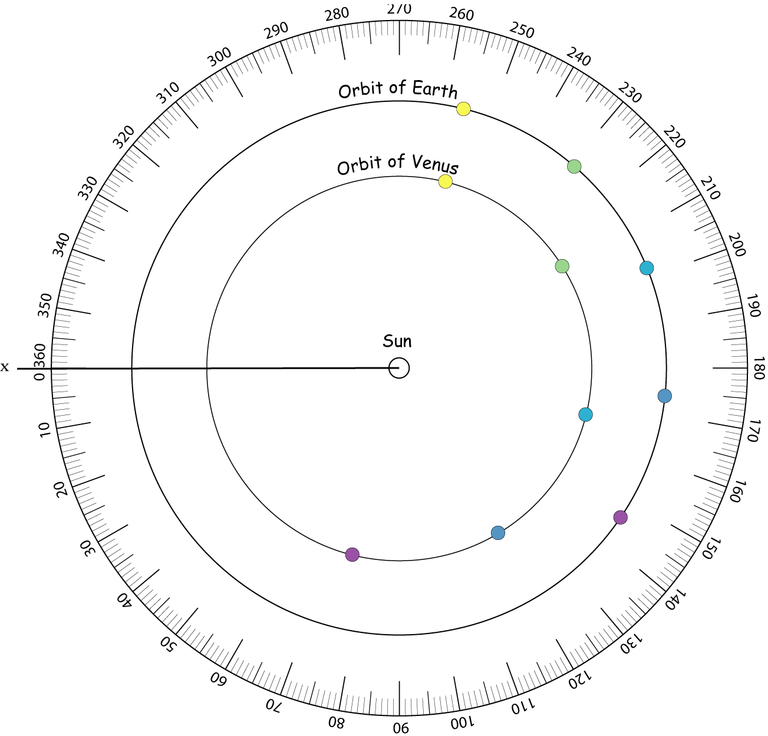
- The chosen direction [Sx) serves as an origin. Place the Earth and Venus in their orbits for the five dates in the table below (you may colour code the dates).
The given angle is the angle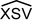 (V is Venus) or
(V is Venus) or 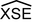 (E is the Earth) measured anticlockwise.
(E is the Earth) measured anticlockwise.
Angle 15/02/2012 14/03/2012 11/04/2012 09/05/20120 06/06/2012 Venus 
76° 121° 166° 212° 256° Earth 
146° 174° 202° 229° 256° - Using the figure, measure the angle Venus Earth Sun on February the 15th and April the 11th.
- What will happen on June the 6th?
Figure which may be distributed to pupils
2. Maximal elongation of Vénus
Prerequisite knowledge: scales, trigonometry, Pythagorean Theorem.
Taking the problem in toto, Earth and Venus are assumed to revolve around the Sun in the same plane, on circular orbits, and at a constant speed.
Note: RE is the radius of the Earth's orbit (in km), RV the radius of the orbit of Venus (in km), PE and PV periods or respective times of revolution of the Earth and Venus (in days).
Take: RE = 150,000,000 ; RV = 108,000,000; PE = 365, PV = 225.
- Write RE et RV in scientific notation with two significant digits (in km).
- Make a diagram using the scale 1/1013 representing the orbits of two planets. Note that the Sun will be represented by S.
- Venus and Earth have essentially the same diameter (between 12,000 and 13,000 km). Calculate what the diameter would be on this scale
- In this diagram, note that E is the position of the Earth at any point in its orbit, V1 Venus’s closest position to Earth ("inferior conjunction") and V2 the most distant position ("superior conjunction"). Calculate the distances EV1 and EV2.
- Place Venus in the diagram (position V3) so that the angle
 is as large as possible ("maximal elongation"). Calculate the distance EV3 and the angle
is as large as possible ("maximal elongation"). Calculate the distance EV3 and the angle  .
. - Next, imagine how Venus would appear in position V3 through a telescope (look for the part of Venus illuminated by the Sun).
- The same apparent position of Venus (for instance, an inferior conjunction) returns every 584 days. Calculate the number of revolutions completed by the Earth and Venus around the Sun in the meantime. Conclusion.
Additional questions (more difficult)
- When Copernicus developed his system of the world, he knew the period of revolution of the Earth (365 days) and the apparent period of Venus (584 days = synodic period), but he wasn’t aware of the sidereal period of Venus.
To determine, as he did, the period of revolution of Venus x:
- Calculate the number of revolutions N1 made by the Earth in 584 days.
- Calculate, according to x, the number of revolutions N2 made by Venus in 584 days.
- After 584 days, these three celestial bodies have the same relative positions: therefore Venus has made one more orbit around the Sun than the Earth has .Thus we have: N2 = N1 + 1.
Deduce x. - Calculate the angular diameter of Venus at the time of inferior conjunction, elongation and superior conjunction (in arc seconds).
The angular diameter is the angle subtended by the diameter of Venus as observed from Earth.

3. Distance of Venus
Prerequisite knowledge: metric relations in any triangle.
If Venus is observed at 30 ° from the Sun, how far is it from us?
Data:
Distance Earth - Sun: 150,000,000 km.
Distance Venus - Sun: 108,000,000 km.
It is assumed that the planetary orbits are circular, coplanar and centered on the Sun.
4. Distance of Venus and function
The task is to write and represent the distance from Earth to Venus as a function of time.
An inferior conjunction of Venus (Venus-Earth-Sun alignment) is the chosen starting point and it is assumed that orbits are circular and the speed of travel is constant.
Data:
Radius of Venus’ orbit: 108,000,000 km. Period: 225 days
Radius of Earth's orbit: 150,000,000 km. Period: 365 days
5. Sidereal period and synodic period
On the 6th of June 2012, the Sun, Venus and Earth will align in that order. We are going to look for a date when there will be another such alignment.
Data:
Period of revolution of the Earth: 365.26 days
Period of revolution of Venus: 224.7 days
It is assumed that planetary orbits are circular, heliocentric, coplanar; and the speed of travel is constant and in the same direction.
(Exercises 2, 3 and 4 are extracted from the occasional Math and Astronomy, Comité de Liaison Enseignants et Astronomes, clea-astro.eu)
6. Speed and density of Venus
Data:
Sidereal rotation period of Venus: 225 days;
Mean distance from Sun: 108,200,000 km;
Radius of the planet: 6,052 km;
Mass: 4.87 × 1024 kg.
From these data, calculate:
- The average speed of Venus, assuming its orbit is circular.
- Its density.
Solutions
1. Venus and Earth in their orbits
4. Angle Venus Earth Sun on the 15th of February : 42° ; on the 11th of april : 45 °
5. On the 6th of June, Venus will be seen in front of the Sun
2. Maximal elongation of Vénus
- RE = 1.5×108 km ; RV = 1.08×108 km.
- On the same scale, the diameter of the Earth would be about 1 micron!
- EV1 = 42,000,000 km ; EV2 = 258,000,000 km.
- The maximum elongation is obtained by plotting the tangent to the orbit of Venus.
EV3 is calculated with the Pythagorean theorem (104 million km).
We obtain, using sine, an angle of 46°.
In fact, the orbits are not perfectly circular and the maximum elongation of Venus is between 45° and 47° 45 '. - Venus appears in quarter phase as a half disk.
- In 584 days, Venus performs 2.6 revolutions and the Earth 1.6, one revolution less. Therefore, seen from Earth, Venus will be found in the same position relative to the Sun.
The rotation periods of 225 days for Venus and 365 days for the Earth are sidereal periods measured relative to the stars which are considered fixed. The apparent period of 584 days is called Venus’s synodic period. - N1 = 584/365 and N2 = 584/x.
The equation becomes: 584/x = 584/365 + 1 then 1/x = 1/365 + 1/584.
We get 587 days instead of 584 due to approximations. To get a more accurate result, use 224.7 days and 365.3 days instead of 225 and 365.
Note: the equation 1/x = 1/365 + 1/584 can be interpreted as a composition of angular velocities in revolutions/day. It means that the angular velocity of Venus relative to the stars (1/x or 1/225) is equal to the angular velocity of Venus relative to Earth (1/584) plus the angular velocity of Earth relative to the stars (1/365). - Most of the time, pupils tend to use the tangent, either by dividing the isosceles triangle into two right-angled triangles, or by equating the isosceles triangle with a right-angled triangle. The difference is not significant.
We can also do these calculations without trigonometry, by confusing the diameter of Venus with an arc whose length is proportional to the angle at the center.
When r is the distance between Earth and Venus in km: 2 r → 360° then 12100 → 360° × 12100/2
r → 360° then 12100 → 360° × 12100/2  r
r
By multiplying by 3600 to get arc seconds, we get the formula: apparent diameter a (in arc seconds) ≈ 2496 x 106/r
We get as the apparent diameter of Venus, about 10" at the superior conjunction, 24" at the greatest elongation, and 59" at the inferior conjunction. Unfortunately at this time, the unlit side of Venus is facing the Earth.
3. Distance of Venus
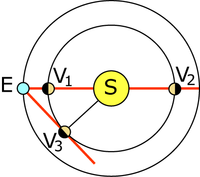
In the triangle Sun-Earth-Venus, known SV (108), SE (150) and ![]() (30°). We are looking for EV.
(30°). We are looking for EV.
Here we are looking for the distance from center to center, the radiuses of the planets are small compared to their distance.
A diagram immediately shows that there are two solutions.
Method 1 with al Kashi :
SV² = SE² + VE² – 2×SE×VE×cos ![]() ; 108² = 150² + VE² – 2 × 150 × VE × cos30°
; 108² = 150² + VE² – 2 × 150 × VE × cos30°
VE is a solution to the equation VE² – 150 × ![]() VE + 10836 = 0. There are two solutions : VE = 75
VE + 10836 = 0. There are two solutions : VE = 75 ![]() ±
± ![]() ⇒ VE = 52.2 or 207.6 million km.
⇒ VE = 52.2 or 207.6 million km.
Method 2 with the sine law :
sin ![]() = (150/108) × sin30° then sin
= (150/108) × sin30° then sin ![]() = 25/36. We find two solutions: 44° ou 136°.
= 25/36. We find two solutions: 44° ou 136°.![]() = 180° – 30° –
= 180° – 30° – ![]() .
. ![]() is 14° ou 106°. We apply the sine law again.
is 14° ou 106°. We apply the sine law again.
VE = 108 × (sin ![]() / sin
/ sin ![]() ) = 216 x sin
) = 216 x sin ![]() ⇒ VE = 52.3 or 207.6 million km.
⇒ VE = 52.3 or 207.6 million km.
4. Distance of Venus and function
Origin of the angles: Sun-Earth direction at the conjunction.
The angle origin - Sun - Earth is 360 ° × t/365
The angle origin - Sun - Venus is 360 ° × t/225
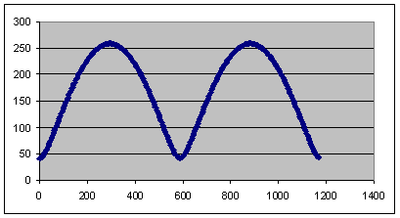
The angle Earth-Sun Venus is (360° × t/225) – (360° × t/365) which represents about 0.614 t (in degrees)
or (2 ![]() × t/225) – (2
× t/225) – (2 ![]() × t/365) which represents about 0.0107 t (in radians)
× t/365) which represents about 0.0107 t (in radians)
We use Al Kashi’s theorem in the Sun Earth Venus triangle.
EV² = 108² + 150² – 2×108×150×cos(0.614 t)
then EV = squareroot (34164 – 32400×cos (0.614 t))
5. Sidereal period and synodic period
The wording here is deliberately very short and the solution is not easy to find. You can use a simulation with dynamic geometry software to help you to understand the problem (see for example the file xxx).
First method:
Start time: June 6, 2012; angles: the half-line Sun-Earth that very day.
Where t is time in days.
Number of revolutions of the Earth: t/365.26
Number of revolutions of Venus: t/224.7
When the two planets meet in the same configuration, Venus will have made one more revolution than the Earth. Thus we can write: t/224.7= t/365.26 + 1.
Solving this equation gives t ≈ 584 days
Second method:
Angular velocity of Venus: 1/224.7 revolutions/day; Earth: 1/365, 26 revolutions/day;
of Venus from the Earth: 1/224.7 – 1/365.26 (the angular velocities are avoided because the two planets rotate in the same direction).
If we call T the period sought, we have: 1/T = 1/224.7 – 1/365.26 ⇒ T ≈ 584 days.
6. Speed and density of Venus
- Velocity : 2 ×
 × 108,200,000 km / (225 × 24 × 3600 s) ≈ 35 km/s
× 108,200,000 km / (225 × 24 × 3600 s) ≈ 35 km/s - Volume : 4/3 ×
 × (6052)3 ≈ 9.285 × 1011 km3 or 9.285 × 1026 cm3
× (6052)3 ≈ 9.285 × 1011 km3 or 9.285 × 1026 cm3
Relative density : 4.87×1027 g / 9.285 × 1026 cm3 ≈ 5.2 g/cm3
Document Actions