Mathématiques
1. Vénus et la Terre sur leurs orbites
Notions nécessaires : échelles, tracé d’un angle
On veut représenter les positions de Vénus et de la Terre au début de l’année 2012. La distance du Soleil à Vénus est de 108 000 000 km, celle du Soleil à la Terre est de 150 000 000 km.
On choisit comme échelle 1 cm pour 20 000 000 km.
a. Calculer les distances Soleil - Vénus et Soleil - Terre à cette échelle.
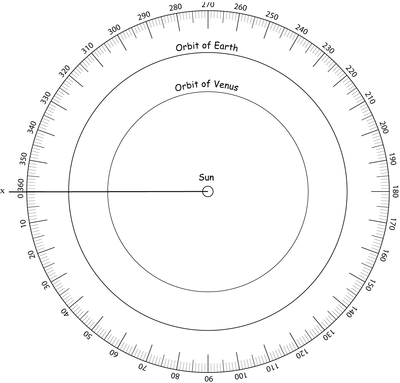
b. Sur une feuille suffisamment grande, placer un point S pour le Soleil puis représenter les orbites de Vénus et de la Terre par un cercle centré sur S à cette échelle.
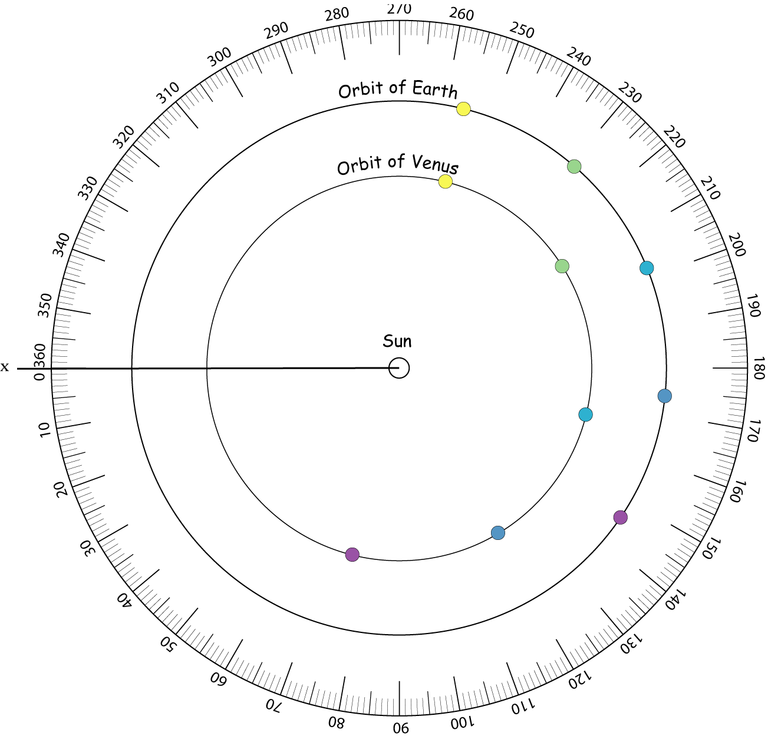
c. On choisit une direction [Sx) qui sert d’origine. Placer ensuite la Terre et Vénus sur leurs orbites pour les cinq dates indiquées dans le tableau ci-dessous (on pourra prendre une couleur par date).
L’angle donné est l’angle xSV (V est Vénus) ou xST (T est la Terre) mesuré dans le sens inverse des aiguilles d’une montre.
| Angle | 15/02/2012 | 14/03/2012 | 11/04/2012 | 09/05/20120 | 06/06/2012 | |
| Venus |  |
76° | 121° | 166° | 212° | 256° |
| Terre |  |
146° | 174° | 202° | 229° | 256° |
Longitude écliptique de Vénus et de la Terre du 15 février au 6 juin 2012
d. En utilisant la figure, mesurer l’angle Vénus Terre Soleil le 15 février, puis 11 avril.
e. Que va-t-il se passer le 6 juin ?
Figure à distribuer éventuellement aux élèves :
2. Élongation maximale de Vénus
Notions nécessaires : échelles, trigonométrie, théorème de Pythagore
Dans tout le problème, on suppose que la Terre et Vénus tournent autour du Soleil dans le même plan en suivant des orbites circulaires à vitesse constante.
On notera RT le rayon de l'orbite terrestre (en km), RV le rayon de l'orbite de Vénus (en km), PT et PV les périodes ou durées de révolution respectives de la Terre et Vénus (en jours).
On prendra : RT = 150 000 000 ; RV = 108 000 000 ; PT = 365 ; PV = 225.
- Écrire RT et RV en notation scientifique.
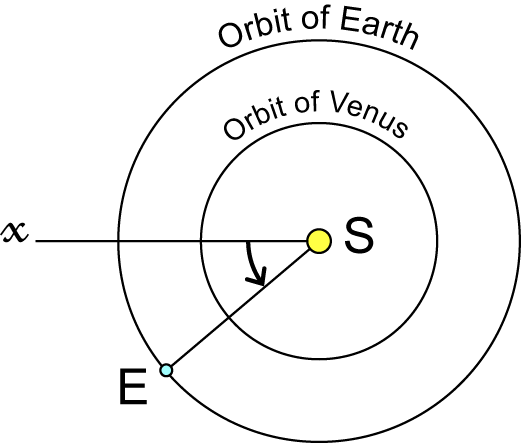
- Faire un schéma à l'échelle 1/1013 représentant les orbites des deux planètes. On notera S le Soleil.
- Vénus et la Terre ont sensiblement le même diamètre (entre 12 000 et 13 000 km). Calculer ce que deviendrait ce diamètre à cette échelle.
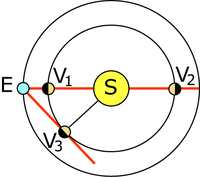
- Sur ce schéma, noter T la position de la Terre à un endroit quelconque de son orbite, V1 la position de Vénus la plus proche de la Terre ("conjonction inférieure") et V2 la plus lointaine ("conjonction supérieure"). Calculer TV1 et TV2.
- Placer Vénus sur le schéma (position V3) pour que l'angle STV soit le plus grand possible ("élongation maximale"). Calculer alors la distance TV3 et l'angle STV3.
- Imaginez ensuite comment apparaît Vénus en V3 dans un télescope (chercher la partie de Vénus éclairée par le Soleil).
- Une même position apparente de Vénus (par exemple une conjonction inférieure) revient tous les 584 jours. Calculer le nombre de tours effectués par la Terre puis par Vénus autour du Soleil pendant ce temps. Conclure.
Questions supplémentaires (plus difficile)
1) Quand Copernic élabora son système du monde, il ne connaissait que la période de révolution de la Terre de 365 jours et la période apparente de 584 jours (période synodique de Vénus) mais ignorait la période de révolution sidérale de Vénus.
Pour déterminer, comme lui, la période x de révolution de Vénus:
- Calculer le nombre de tours N1 effectués par la Terre en 584 jours.
- Calculer, en fonction de x, le nombre de tours N2 effectués par Vénus en 584 j.
- On retrouve les mêmes positions relatives des trois astres après 584 jours, donc Vénus a fait un tour de plus que la Terre autour du Soleil. On a donc : N2 = N1+1.
En déduire x.
2) Calculer le diamètre angulaire de Vénus à l'époque de la conjonction inférieure, de l'élongation maximale et de la conjonction supérieure (en secondes d'arc).
Le diamètre angulaire est l'angle a sous lequel on voit le diamètre de Vénus depuis la Terre.
(Cet exercice est extrait du hors série Maths et astronomie, Comité de Liaison Enseignants et Astronomes)
Solutions
1. Venus et la Terre sur leurs orbites
d. Angle Vénus Terre Soleil le 15 février : 42° ; le 11 avril : 45°.
e. Le 6 juin, on verra Vénus devant le Soleil.
2. Elongation maximale de Vénus
- RE = 1.5×108 km ; RV = 1.08×108 km.
2. a. RT = 1,5×108 ; RV = 1,08×108 .
c. À la même échelle, le diamètre de la Terre serait d'environ 1 micromètre !
d. TV1 = 42 000 000 km ; TV2 = 258 000 000 km.
e. L'élongation maximale est obtenue en traçant la tangente à l'orbite de Vénus.
On calcule TV3 avec le théorème de Pythagore (104 millions de km).
On obtient, avec le sinus, un angle de 46°.
En réalité, les orbites ne sont pas tout à fait circulaire et l’élongation maximale de Vénus varie entre 45° et 47° 45’.- f. Vénus apparaît en quartier sous la forme d'un demi disque.
g. En 584 jours, Vénus effectue 2,6 tours et la Terre 1,6 tour, soit un tour de moins. Vue depuis la Terre, on retrouvera donc Vénus dans la même position par rapport au Soleil.
Les périodes de révolution de 225 jours pour Vénus ou 365 jours pour la Terre sont des périodes sidérales, mesurées par rapport aux étoiles considérées comme fixes. La période apparente de 584 jours de Vénus est appelée période synodique.
h. N1 = 584/365 et N2 = 584/x.
L'équation devient : 584/ x = 584/365 + 1 ou 1/ x = 1/365+ 1/584
On obtient 587 jours au lieu de 584 à cause des approximations. Pour avoir un résultat plus précis, il suffit de prendre 224,7 j et 365,3 j au lieu de 225 et 365.
Remarque : l'équation 1/x = 1/365 + 1/584 peut s'interpréter comme une composition de vitesses angulaires en tours/jour. Elle signifie que la vitesse angulaire de Vénus par rapport aux étoiles (1/ x ou 1/225) est égale à la vitesse angulaire de Vénus par rapport à la Terre (1/584) plus la vitesse angulaire de la Terre par rapport aux étoiles (1/365).
i. Les élèves pensent la plupart du temps à utiliser la tangente, soit en partageant le triangle isocèle en 2 triangles rectangles, soit en assimilant le triangle isocèle à un triangle rectangle. La différence n'est pas significative.
On peut aussi faire ces calculs sans trigonométrie, en confondant le diamètre de Vénus avec un arc de cercle dont la longueur est proportionnelle à l'angle au centre.
En appelant r la distance Terre-Vénus en km : 2
r → 360° then 12100 → 360° × 12100/2 r
En multipliant par 3600 pour obtenir des secondes d'arc, on obtient la formule :
Diamètre apparent a (en secondes d'arc) ≈ 2496 x 106/r
On obtient comme diamètre apparent de Vénus, environ 10" à la conjonction supérieure, 24" à l'élongation maximale et 59" à la conjonction inférieure. Malheureusement à ce moment, c'est le côté non éclairé de Vénus qui fait face à la Terre.
3. Distance de Vénus
Dans le triangle Soleil Terre Vénus, on connaît SV (108), ST (150) et 
(30°). On cherche TV.
On cherche ici une distance de centre à centre, le rayon des planètes étant petit devant leur distance.
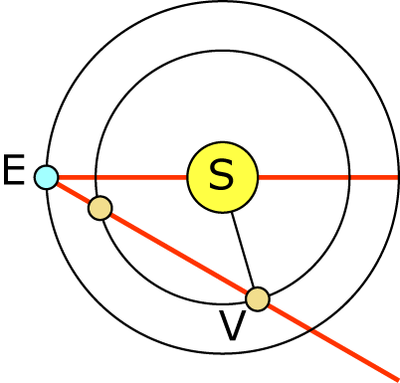
Un schéma montre tout de suite qu'il y a deux solutions.
Méthode 1 avec al Kashi :
SV² = SE² + VE² – 2×SE×VE×cos ; 108² = 150² + VE² – 2 × 150 × VE × cos30°
VE est solution de l'équation VE² – 150 × 
VE + 10836 = 0. On trouve deux solutions : VE = 75 ± 
⇒ VE = 52.2 ou 207.6 million km.
Methode 2 avec la loi des sinus :
sin
= (150/108) × sin30° then sin = 25/36. Deux solutions 44° ou 136°
= 180° – 30° – . is 14° ou 106°. On applique à nouveau la loi des sinus VE = 108 × (sin
/ sin 
) = 216 x sin ⇒ VE = 52.3 soit 207.6 million km.
4. Distance of Venus and function
Origine des angles : la direction Soleil Terre lors de la conjonction.
L'angle origine - Soleil - Terre vaut 360°×t / 365
L'angle origine - Soleil - Vénus vaut 360°×t / 225
L'angle Terre Soleil Vénus vaut 360° × t / 225 – 360° × t / 365 soit environ 0,614 t (en degrés)
ou (2 × t/225) – (2 × t/365) which represents about 0.0107 t (in radians)
On utilise le théorème d’al Kashi dans le triangle Soleil Terre Vénus
TV² = 108² + 150² -2×108×150×cos (0,614 t)
d'où TV = racine(34 164 - 3 240 cos (0,614 t))
5. Période sidérale et période synodique
L'énoncé est ici volontairement très court et la solution n'est pas simple à trouver. On peut utiliser une simulation avec un logiciel de géométrie dynamique pour mieux comprendre le problème (voir par exemple le fichier xxx).
Première méthode :
Origine des temps : 6 juin 2012 ; des angles : la demi-droite Soleil Terre ce jour-là.
On note t le temps en jour.
Nombre de tours effectués par la Terre : t/365,26
Nombre de tours effectués par Vénus : t/224,7
Quand les deux planètes se retrouveront dans la même configuration, Vénus aura effectué un tour de plus que la Terre. On peut donc écrire : t/224,7 = t/365,26 + 1.
La résolution de cette équation donne t ≈ 584 jours
Deuxième méthode :
Vitesse angulaire de Vénus : 1/224,7 tour/jour ; de la Terre : 1/365,26 tour/jour ;
de Vénus par rapport à la Terre : 1/224,7 - 1/365,26 (les vitesses angulaires se soustraient car les deux planètes tournent dans le même sens).
Si on appelle T la période recherchée, on doit avoir : 1/T = 1/224,7 - 1/335,26.
6. Vitesse et masse volumique de Vénus
- Vitesse : 2 × × 108,200,000 km / (225 × 24 × 3600 s) ≈ 35 km/s
- Volume : 4/3 × × (6052)3 ≈ 9.285 × 1011 km3 or 9.285 × 1026 cm3
Masse volumique : 4.87×1027 g / 9.285 × 1026 cm3 ≈ 5.2 g/cm3
Actions sur le document
